This CVPR paper is the Open Access version, provided by the Computer Vision Foundation. Except for this watermark, it is identical to the accepted version; the final published version of the proceedings is available on IEEE Xplore.

Generalized Event Cameras

Varun Sundar† Matthew Dutson † Andrei Ardelean vsundar4@wisc.edu dutson@wisc.edu a.ardelean@epfl.ch Claudio Bruschini§ Edoardo Charbon§ Mohit Gupta† {claudio.bruschini, edoardo.charbon}@epfl.ch mohitg@cs.wisc.edu †University of Wisconsin- Madison ‡NovoViz §École Polytechnique Fédérale de Lausanne wisionlab.com/project/generalized- event- cameras/

Abstract

Event cameras capture the world at high time resolution and with minimal bandwidth requirements. However, event streams, which only encode changes in brightness, do not contain sufficient scene information to support a wide variety of downstream tasks. In this work, we design generalized event cameras that inherently preserve scene intensity in a bandwidth- efficient manner. We generalize event cameras in terms of when an event is generated and what information is transmitted. To implement our designs, we turn to single- photon sensors that provide digital access to individual photon detections; this modality gives us the flexibility to realize a rich space of generalized event cameras. Our single- photon event cameras are capable of high- speed, high- fidelity imaging at low readout rates. Consequently, these event cameras can support plug- and- play downstream inference, without capturing new event datasets or designing specialized event- vision models. As a practical implication, our designs, which involve lightweight and near- sensor- compatible computations, provide a way to use single- photon sensors without exorbitant bandwidth costs.

1. Introduction

Event cameras [6, 34, 44] sense the world at high speeds, providing visual information with minimal bandwidth and power. They achieve this by transmitting only changes in scene brightness, when significant "events" occur. However, there is a cost. Raw event data, a sparse stream of binary values, does not hold sufficient information to be used directly with mainstream vision algorithms. Therefore, while event cameras have been successful at certain tasks (e.g., object tracking [15, 33], obstacle avoidance [7, 20, 49], and high- speed odometry [12, 21, 68]), they are not widely deployed as general- purpose vision sen sors, and often need to be supplemented with conventional cameras [14, 15, 21]. These limitations are holding back this otherwise powerful technology.

Is it possible to realize the promise of event cameras, i.e., high temporal resolution at low bandwidth, while preserving rich scene intensity information? To realize these seemingly conflicting goals, we propose a novel family of generalized event cameras. We conceptualize a space of event cameras along two key axes (Fig. 1 (top)): (a) "when to transmit information," formalized as a change detection procedure $\Delta$ ; and (b) "what information to transmit," characterized by an integrator $\Sigma$ that encodes incident flux. Existing event cameras represent one operating point in this $(\Sigma , \Delta)$ space. Our key observation is that by exploring this space and considering new $(\Sigma , \Delta)$ combinations, we can design event cameras that preserve scene intensity. We propose more general integrators, e.g., that represent flux according to motion levels, that span spatial patches, or that employ temporal coding (Fig. 1 (middle)). We also introduce robust change detectors that better distinguish motion from noise, by considering increased spatiotemporal contexts and modeling noise in the sensor measurements.

Despite their conceptual appeal, physically implementing generalized event cameras is a challenge. This is because the requisite computations must be performed at the sensor to achieve the desired bandwidth reductions. For example, existing event cameras perform simple integration and thresholding operations via analog in- pixel circuitry. However, more general $(\Sigma , \Delta)$ combinations are not always amenable to analog implementations; even feasible designs might require years of hardware iteration and production scaling. To build physical realizations of generalized event cameras, we leverage an emerging sensor technology: single- photon avalanche diodes (SPADs) that provide digital access to photon detections at extremely high frame rates ( $\sim 100 \mathrm{kHz}$ ). This allows us to compose arbitrary software- level signal transformations, such as those required by generalized event cameras. Further, we are not locked to a particular event camera design and can realize multiple configurations

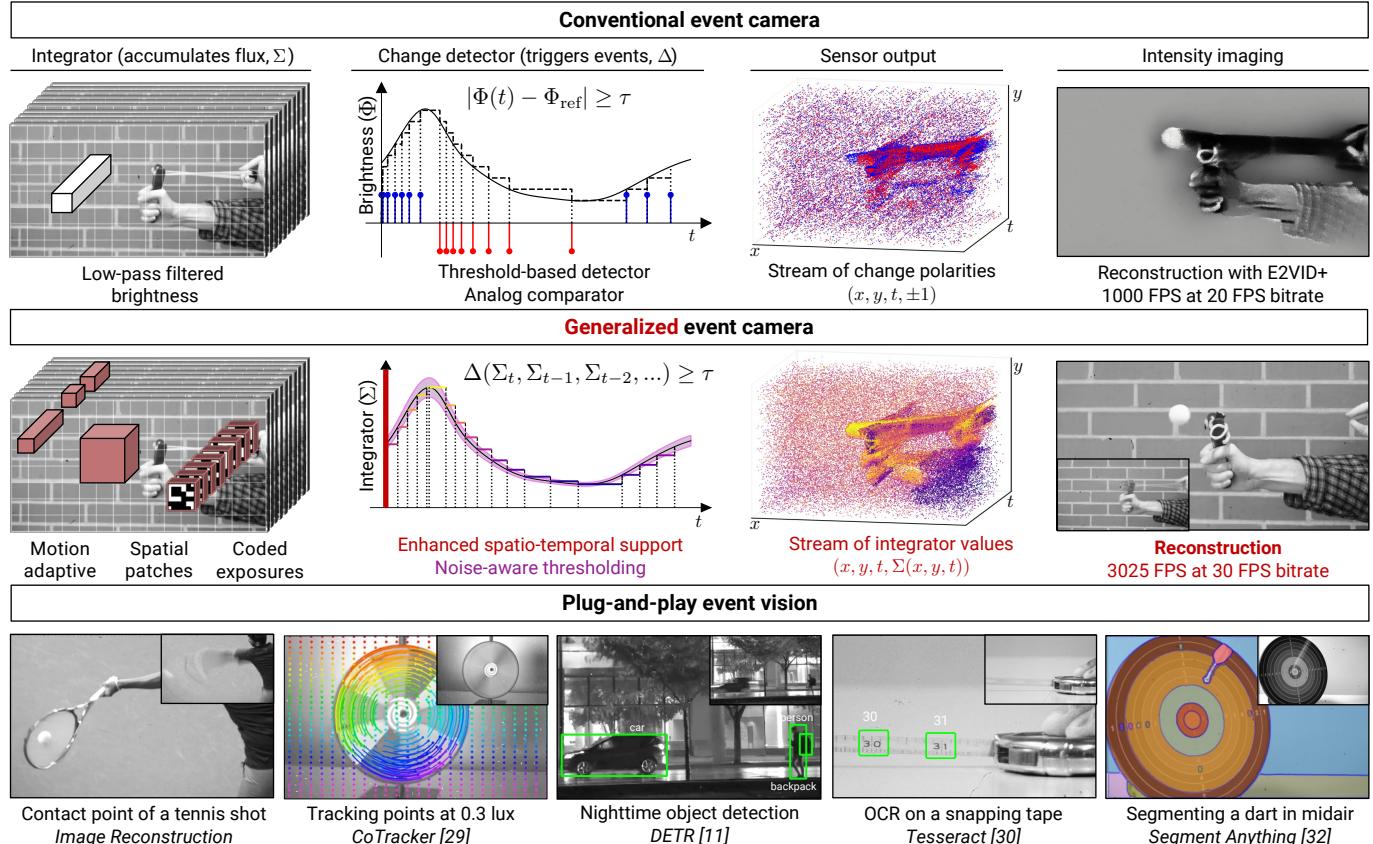
Figure 1. Generalized event cameras. (top) Event cameras generate outputs in response to abrupt changes in scene intensity. We describe this as a combination of a low-pass integrator and a threshold-based change detector. (middle) We generalize the space of event cameras by designing integrators that capture rich intensity information, and more reliable change detectors that utilize larger spatiotemporal contexts and noise-aware thresholding (Secs. 4.1 to 4.3). Unlike existing events, our generalized event streams inherently preserve scene intensity, e.g., this ping-pong ball slingshotted against a brick wall backdrop. (bottom) Generalized event cameras enable high-fidelity bandwidth-efficient imaging: providing 3025 FPS reconstructions with a readout equivalent to a 30 FPS camera. Consequently, generalized events facilitate plug-and-play inference on a multitude of tasks in challenging scenarios (insets depict the extent of motion over $30~\mathrm{ms}$ ).

with the same sensor.

Implications: extreme, bandwidth- efficient vision. Generalized event cameras support high- speed, high- quality image reconstruction, but at low bandwidths quintessential of current event cameras. For example, Fig. 1 (middle, bottom) shows reconstructions at 3025 FPS that have an effective readout of a 30 FPS frame- based camera. Further, our methods have strong low- light performance due to the SPAD's single- photon sensitivity. As we show in Fig. 1 (bottom), preserving scene intensity facilitates plug- and- play inference in challenging scenarios, with state- of- the- art vision algorithms. Critically, this does not require retraining vision models or curating dedicated datasets, which is a significant challenge for unconventional imagers. This plug- and- play capability is vital to realizing universal event vision that retains the benefits of current event cameras.

Scope. We consider full- stack event perception: we conceptualize a novel space of event cameras, provide relevant single- photon algorithms, analyze their imaging capabilities and ratedistortion trade- offs, and show on- chip feasibility. We demon strate imaging capabilities in Secs. 5.1 and 5.2 using the SwissSPAD2 array [62], and show viable implementations of our algorithms for UltraPhase [4], a recent single- photon compute platform. All of these are critical to unlocking the promise of event cameras. However, our objective is not to develop an integrated system that incorporates all these components; this paper merely takes the first steps toward that goal.

2. Related Work

Event camera designs. Perhaps most widespread is the DVS event camera [34], where each pixel generates an event in response to measured changes in (log) intensity. The DAVIS event camera [6, 9] couples DVS pixels with conventional CMOS pixels, providing access to image frames. However, the frames lack the dynamic range of DVS events. A recent design, Celex- V [23], provides log- intensity frames using an external trigger. ATIS [44], a less prevalent design, features asynchronous intensity events, but its sophisticated circuitry reduces pixel fill factor. The above designs are based on analog processing; we instead

design event cameras on digital photon detections.

Intensity imaging with event cameras. Several approaches have been explored to obtain images from events, including Poisson solvers [5], manifold regularization [39], assuming knowledge of camera motion [13, 31] or optical flow [67], and learning- based methods [43, 46, 51, 58, 69]. However, because events often lack sufficient scene information, they are often supplemented by conventional frames [10, 41, 50, 53], either from sensors such as DAVIS or using a multi- camera setup. Fusing events and frames presents challenges due to potential spatiotemporal misalignment and discrepancies in imaging modalities. Even when these challenges are overcome, we show that fusion methods produce lower fidelity than our proposed generalized event cameras.

Passive single- photon imaging. In the past few years, SPADs have found compelling passive imaging applications; this includes high- dynamic range imaging [26, 27, 35, 40], motion deblurring [28, 36, 37, 52], high- speed tracking [17], and ultra wide- band videography [65]. The fine granularity of passive single- photon acquisition makes it possible to emulate a diverse set of imaging modalities [60], including event cameras, via post- capture processing. In this work, we go beyond emulating existing event cameras and design alternate event cameras that preserve high- fidelity intensity information.

3. What is an Event Camera?

The defining characteristic of event cameras is that they transmit information selectively, in response to changes in scene content. This selectivity allows event cameras to encode scene information at high time resolutions required to capture scene dynamics, without proportionately high bandwidth. This is in contrast to frame- based cameras, where readout occurs at fixed intervals.

We characterize event cameras in terms of two axes: what the camera transmits and when it transmits. As a concrete example, consider existing event cameras. They trigger events ("when to transmit") based on a fixed threshold:

$$ |\Phi (\mathbf{x},t) - \Phi_{\mathrm{ref}}(\mathbf{x})|\geq \tau , \tag{1} $$

where $\Phi (\mathbf{x},t)$ is a flux estimate at pixel $\mathbf{x}$ and time $t$ , and $\tau$ is the threshold. $\Phi_{\mathrm{ref}}(\mathbf{x})$ is a previously- recorded reference, set to $\Phi (\mathbf{x},t)$ whenever an event is triggered. Each event consists of a packet

$$ (\mathbf{x},t,\mathrm{sign}(\Phi (\mathbf{x},t) - \Phi_{\mathrm{ref}}(\mathbf{x}))) \tag{2} $$

that encodes the polarity of the change ("what to transmit").

Event polarities, although adequate for some applications, do not retain sufficient information to support a general set of computer vision tasks. A stream of event polarities is an extremely lossy representation. Notably, it only defines scene intensity up to an initial unknown reference value, and it does not encode any information in regions not producing events, i.e., regions with little or no motion.

Figure 2. Altering "what to transmit." (a) We sum the events generated by a jack-in-the-box toy as it springs up. This sum gives a lossy encoding of brightness changes in dynamic regions. (b) Transmitting levels instead of changes helps recover details in static regions. (c) Adaptive exposures, which accumulate flux between consecutive events, provide substantial noise reduction.

Our key observation is that existing event cameras represent just one operating point in a broader space of generalized event cameras, which is defined by two axes: "what to transmit" and "when to transmit." By considering alternate points in this space, we can design event cameras that preserve high- fidelity scene intensity. This enables plug- and- play inference with a host of algorithms developed by the mainstream vision community.

We begin with a conceptual exploration of this generalized space, before describing its physical implementation.

Generalizing "what to transmit." As a first step, we can modify the event camera such that it transmits $n$ - bit values instead of one- bit change polarities. When an event is triggered, we send the current value of $\Phi (\mathbf{x},t)$ ; if a pixel triggers no events, we transmit $\Phi$ during the final readout. As we show in Fig. 2 (b), this simple change allows us to recover scene intensity, even in static regions. It is important to note that, while the transmitted quantity differs from conventional events, we retain the defining feature of an event camera: selective transmission based on scene dynamics (where we transmit according to Eq. (1)). Thus, the readout remains decoupled from the time resolution.

If $\Phi (\mathbf{x},t)$ were a perfect estimate of scene intensity, then the changes thus far would suffice. However, $\Phi$ is fundamentally noisy: to capture high- speed changes, $\Phi$ must encompass a shorter duration, which leads to higher noise. This is a manifestation of the classical noise- blur tradeoff.

To address this problem, we introduce the abstraction of an integrator (or $\Sigma$ ), that defines how we accumulate incident flux and, in turn, what we transmit. Ideally, we want the integrator to adapt to scene dynamics, i.e., accumulate over longer durations when there is less motion, and vice versa. We observe that event generation, which is based on scene dynamics, can be used to formulate an adaptive integrator. Specifically, we propose an integrator $\Sigma_{\mathrm{cum}}$ that computes the cumulative flux since the last event:

$$ \Sigma_{\mathrm{cum}}(\mathbf{x},t) = \int_{T_0}^t\Phi (\mathbf{x},s)ds, \tag{3} $$

where $T_0$ is the time of the last event. When an event is triggered at time $T_1$ , we communicate the value of $\Sigma_{\mathrm{cum}}(\mathbf{x},T_1)$ , which

Event camera	Integrator (Σ)	Change detector (Δ)	Event packets	Min. latency	Intensity info.?	Low-light perf.
Existing (DVS [34])	logarithmic	comparator	binary	10−6to 10−5s	✓	poor
Sec. 4.1	adaptive exposure	Bayesian change detector [2]	scalar	10−5s	✓	good
Sec. 4.2	adaptive exposure	variance-aware differences	patches	10−4s	✓	good
Sec. 4.3	coded exposure	Binomial confidence interval	vector	10−3s	✓	good

Table 1. Summary of generalized event cameras. Our designs integrate photon detections $(\Sigma)$ and detect scene-content changes $(\Delta)$ in distinct ways. We compare our designs to existing DVS event cameras based on their event streams, latencies, and intensity-preserving nature. While providing a direct power comparison to DVS is difficult, we compare the power characteristics among our designs in Sec. 5.4.

we interpret as the intensity throughout $[T_0,T_1]$ . This approach yields a piece- wise constant time series, with segments delimited by events. Adaptive exposures significantly reduce noise, as we show in Fig. 2 (c).

Generalizing "when to transmit." The success of the adaptive integrator crucially depends on the reliability of events; for example, triggering false events in static regions causes unnecessary noise. We refer to the event- generation procedure as the change detector, denoted by $\Delta$ . Current event cameras detect changes by applying a fixed threshold to measured intensity differences (Eq. (1)). This method has two key limitations: it only considers the value of $\Phi$ at pixel location $\mathbf{x}$ and time $t$ , and it is not attuned to the stochasticity in $\Phi$ .

We design more robust change detectors that (1) leverage enhanced spatiotemporal contexts, and (2) incorporate noise awareness, either explicitly by tuning thresholds, or implicitly by modulating the detector's behavior. Specifically, we improve reliability by using temporal forecasters (Sec. 4.1), by leveraging correlated changes in patches (Sec. 4.2), or by exploiting integrator statistics (Sec. 4.3).

Realizing generalized event cameras. The critical detail remaining is how we implement our proposed designs in practice. We need direct access to flux estimates at a high time resolution. Conventional high- speed cameras can provide such access, however, they incur substantial per- frame read noise $(\sim 20 - 40e^{- }$ [25]) that grows with frame rate [8].

We turn to an emerging class of single- photon sensors, single- photon avalanche diodes (SPADs [48]), that has witnessed dramatic improvements in device practicality and key sensor characteristics (e.g., array sizes and fill factors) in recent years [38, 62]. SPADs can operate at extremely high speeds $(\sim 100\mathrm{kHz})$ without incurring per- frame read noise. Each $\Phi (\mathbf{x},t)$ measured by a SPAD is limited only by the fundamental stochasticity of photon arrivals (shot noise). This allows SPADs to provide high timing resolution without a substantial noise penalty. In the next section, we describe the image formation model of SPADs and provide single- photon implementations of our designs.

4. Single-Photon Generalized Event Cameras

A SPAD array can operate as a high- speed photon detector, producing binary frames as output. Each binary value indicates whether at least one photon was detected during an expo sure. The SPAD output response, $\Phi (\mathbf{x},t)$ , can be modeled as a Bernoulli random variable, with

$$ P(\Phi (\mathbf{x},t) = 1) = 1 - e^{-N(\mathbf{x},t)}, \tag{4} $$

where $N(\mathbf{x},t)$ is the average number of photo- electrons during an exposure, including any spurious detections. The inherently digital SPAD response allows us to compute software- level transformations on the signal $\Phi (\mathbf{x},t)$ , including operations that may be challenging to realize via analog processing. These transformations can be readily reconfigured, which permits a spectrum of event camera designs, not just one particular choice. However, there is one consideration: our designs should be lightweight and computable on chip. As we show in Sec. 5.4, this is vital to implementing generalized event cameras without the practical costs associated with reading off raw SPAD outputs.

We now describe a set of SPAD- based event cameras (summarized in Tab. 1), beginning with the adaptive exposure method from the previous section.

Adaptive- exposure event camera. We obtain a SPAD implementation of the adaptive exposure described in Eq. (3) by replacing the integral with a sum over photons:

$$ \Sigma_{\mathrm{cum}}(\mathbf{x},t) = \sum_{s = T_0}^{t}\Phi (\mathbf{x},s). \tag{5} $$

To generate events, we can use a threshold- based change detector (Eq. (1)). Differences between individual binary values are not sufficiently informative; therefore, we apply Eq. (1) to an exponential moving average (EMA) computed on $\Phi$ . We call this an "adaptive- EMA" event camera.

4.1. Bayesian Change Detector

A fixed- threshold change detector such as Eq. (1) does not account for the SPAD's image formation model; it uses the same threshold irrespective of the underlying variance in photon detections. As a result, such a detector may fail to detect changes in low- contrast regions without producing a large number of false- positive detections (see Fig. 3 (left)).

In this section, we consider a Bayesian change detector, BOCPD [1], that is tailored to the Bernoulli statistics of photon detections. BOCPD uses a series of forecasters to estimate the likelihood of an abrupt change. At each time step, a new forecaster $\nu_{t}$ is initialized as a recurrence of previous forecasters,

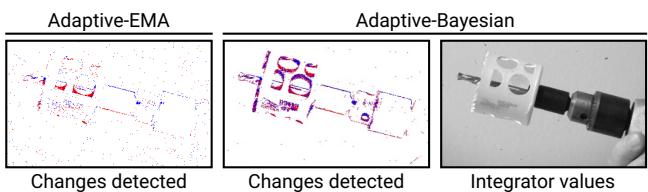
Figure 3. Bayesian- vs. EMA-based change detection. (left) A fixed-threshold change detector (used in adaptive-EMA) makes it difficult to segment low-contrast changes. (center) The Bayesian formulation attunes to the stochasticity in incident flux and can detect fine-grained changes such as the corners of the hole saw bit; (right) as a result, the integrator captures the rotational dynamics.

and existing forecasters are updated:

$$ \nu_{t} = (1 - \gamma)\sum_{s = 1}^{t - 1}l_{s}\nu_{s},\qquad \nu_{s}\gets \gamma l_{s}\nu_{s}\forall s< t, \tag{6} $$

where $\gamma \in [0,1]$ is the sensitivity of the change detector, with larger $\gamma$ resulting in more frequent detections. $l_{s}$ is the predictive likelihood of each forecaster, which we compute by tracking two values per forecaster, $\alpha_{s}$ and $\beta_{s}$ , that correspond to the parameters of a Beta prior. For a new forecaster, these values are initialized to 1 each, reflecting a uniform prior. Existing $(\alpha_{s},\beta_{s}),\forall s< t$ , are updated as

$$ \alpha_{s}\leftarrow \alpha_{s} + \Phi (\mathbf{x},t),\quad \beta_{s}\leftarrow \beta_{s} + 1 - \Phi (\mathbf{x},t). \tag{7} $$

$l_{s}$ is given by $\alpha_{s} / (\alpha_{s} + \beta_{s})$ if $\Phi (\mathbf{x},t) = 1$ , and $\beta_{s} / (\alpha_{s} + \beta_{s})$ otherwise. An event is triggered if the highest- value forecaster does not correspond to $T_{0}$ , the timestamp of the last event; mathematically, if $\mathrm{argmax},\nu_t\neq T_0$

To make BOCPD viable in memory- constrained scenarios, we apply extreme pruning by retaining only the three highest- value forecasters [64]. We also incorporate restarts, deleting previous forecasters when a change is detected [2].

Compared to an EMA- based change detector, the Bayesian approach more reliably triggers events in response to scene changes while better filtering out stochastic variations caused by photon noise—which we show in Fig. 3.

4.2. Spatiotemporal Chunk Events

Sec. 4.1 leverages an expanded temporal context for change detection; however, it treats each pixel independently and does not exploit spatial information. In this section, we devise an event camera with enhanced spatial context that operates on small patches, e.g., of $4\times 4$ pixels. It is difficult to derive efficient Bayesian change detectors for multivariate time series; thus, we adopt a model- free approach that does not explicitly parameterize the patch distribution. To afford computational breathing room for more expensive patch- wise operations, we employ temporal chunking. That is, we average $\Phi (\mathbf{x},t)$ over a small number of binary frames (e.g., 32 binary frames) instead of operating on individual binary frames; generally, this averaging does not induce perceptible blur.

Let vector $\Phi_{\mathrm{chunk}}(\mathbf{y},t)$ represent the chunk- wise average of photon detections at patch location $\mathbf{y}$ . Let vector $\Sigma_{\mathrm{patch}}(\mathbf{y},t)$ be an integrator representing the cumulative mean since the last event, but excluding $\Phi_{\mathrm{chunk}}$ . We want to estimate whether $\Phi_{\mathrm{chunk}}$ belongs to the same distribution as $\Sigma_{\mathrm{patch}}$ . We do so with a lightweight approach, that computes the distance between $\Phi_{\mathrm{chunk}}$ and $\Sigma_{\mathrm{patch}}$ in the linear feature space of matrix $\mathbf{P}$ . As we show in Fig. 4, linear features allow us to capture spatial structure within a patch. Geometrically, $\mathbf{P}$ induces a hyperellipsoidal decision boundary, in contrast to the spherical boundary of the L2 norm.

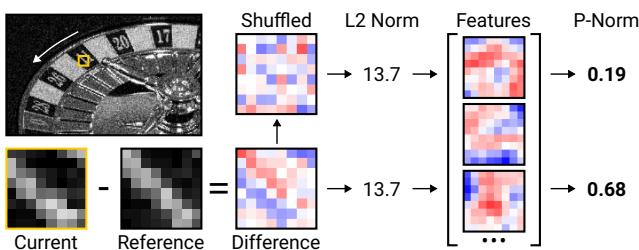
Figure 4. Spatiotemporal chunk events. We evaluate the difference between the current chunk and a stored reference in a learned linear-feature space. Unlike the L2 norm, which is permutation-invariant, the feature-space norm is sensitive to spatial structure. Randomly shuffling the pixel values reduces the transform-domain norm (the shuffled patch has a more "noise-like" structure).

This method generates an event whenever

$$ | \mathbf{P}(\tilde{\Phi}{\mathrm{chunk}}(\mathbf{y},t) - \tilde{\Sigma} $$}}(\mathbf{y},t))| _2\geq \tau , \tag{8

where $\tau$ is the threshold. When there is no event, we extend the cumulative mean to include the current chunk. Before computing linear features, we normalize $\Phi_{\mathrm{chunk}}$ and $\Sigma_{\mathrm{patch}}$ elementwise according to the estimated variance in $\Phi_{\mathrm{chunk}} - \Sigma_{\mathrm{patch}}$ ; we annotate the normalized versions with a tilde. We estimate the variance based on the fact that, in a static patch, the elements of $\Phi_{\mathrm{chunk}}$ and $\Sigma_{\mathrm{patch}}$ are independent binomial random variables.

We train the matrix $\mathbf{P}$ on simulated SPAD data, generated from interpolated high- speed video. We apply backpropagation through time to minimize the MSE error of the transmitted patch values. To address the non- differentiability arising from the threshold, we employ surrogate gradients. Please see the supplementary material for complete details of this method.

4.3. Coded-Exposure Events

In this section, we design a generalized event camera by applying change detection to coded exposures [22, 45, 47], which capture temporal variations by multiplexing photon detections over an integration window. This is interesting in two aspects. First, we are designing event streams based on an modality not typically associated with event cameras. Second, we show that high- speed information can be obtained even when the change detector operates at a coarser time granularity. Coded- exposure events provide somewhat lower fidelity than our designs in Secs. 4.1 and 4.2, but are more compute- and power- efficient, owing to less frequent execution of the change detector.

At each pixel, we multiplex a temporal chunk of $T_{\mathrm{code}}$ $\sim 256-$ 512) binary values with a set of $J$ $(\sim 2 - 6)$ codes $C^j (\mathbf{x},t)\forall 1\leq$ $j\leq J$ producing $J$ coded exposures

$$ \Sigma_{\mathrm{coded}}^j (\mathbf{x},t) = \sum_{s = t - T_{\mathrm{code}}}^t\Phi (\mathbf{x},s)C^j (\mathbf{x},s). \tag{9} $$

The codes $C^j$ are chosen to be random, mutually orthogonal binary masks, each containing $T_{\mathrm{code}} / \max (2,J)$ ones [60].

We exploit the statistics of coded exposures to derive a change detector. Observed that in static regions, $\Sigma_{\mathrm{coded}}^j (\mathbf{x},t)$ are independent and identically distributed (iid) binomial random variables. Thus, we can expect them to lie within a binomial confidence interval of one another. If not, we assume the pixel is dynamic and generate an event. We trigger an event if $\Sigma_{\mathrm{coded}}^j\notin \mathrm{conf}(n,\hat{p})$ for any $j$ . Here, "conf' refers to a binomial confidence interval (e.g., Wilson's score), $n = T_{\mathrm{code}} / J$ draws, and $\begin{array}{r}\hat{p} = \sum_{s}\Phi (\mathbf{x},s) / T_{\mathrm{code}} \end{array}$ is the empirical success probability.

If a pixel is static, we store the sum of the $J$ coded exposures, which is a long exposure, denoted by $\Sigma_{\mathrm{long}}$ . If the pixel remains static across more than one temporal chunk, we extend $\Sigma_{\mathrm{long}}$ to include the entire duration. Whereas, if the pixel is dynamic, we transmit ${\Sigma_{\mathrm{coded}}^j}$ , as well as any previous static intensity encoded in $\Sigma_{\mathrm{long}}$ . Downstream, we can apply coded- exposure restoration techniques [54, 63, 66] to recover intensity frames from the coded measurements.

5. Experimental Results

We demonstrate the capabilities of generalized event cameras using a SwissSPAD2 array [62] with resolution $512\times 256$ which we use to capture one- bit frames at $96.8~\mathrm{kHz}$ .We show the feasibility of our designs on UltraPhase [4], a recent singlephoton computational platform (Sec. 5.4).

Refinement model. For each of our event cameras, we train a refinement model that mitigates artifacts arising from the asynchronous nature of events. This model takes a periodic frame- based sampling of integrator values and outputs a video reconstruction. The sampling rate is configurable; in practice, we set it $\sim 16 - 64\times$ lower than the SPAD rate. We use a denselyconnected residual architecture [63], trained on data generated by simulating photon detections on temporally interpolated [24] high- speed videos from the XVFI dataset [56]. See the supplement for training details.

5.1. Extreme Bandwidth-Efficient Videography

High- speed videography. In Fig. 5, we capture the dynamics of a deformable ball (a "stress ball") using a SPAD, a high- speed camera (Photron Infinicam) operated at 500 FPS, and a commercial event camera (Prophesee EVK4). The high- speed camera suffers from low SNR due to read noise, which manifests as prominent artifacts after on- camera compression. Meanwhile, conventional events captured by Prophesee, when processed by "intensity- from- events" methods such as E2VID+ [57] fail to recover intensities reliably, especially in static regions. We also evaluate EDI [42], a hybrid event- frame method. We consider an idealized variant that operates on SPAD events (obtained via EMA thresholding), which gives perfect event- frame alignment and a precisely known event- generation model. We refine the outputs of EDI using the same model as for our methods. We refer to this idealized, refined version of EDI as "EDI++. While EDI++ recovers more detail than other baselines, there are considerable artifacts in its outputs.

Spatiotemporal chunk (Sec 4.2, 431 bps/pixel, rendered at 3025 FPS) Figure 5. High-speed videography of a stress ball hurled at a coffee mug. (top row) This indoor scene is challenging for existing imaging systems, including: high-speed cameras (SNR-related artifacts), event cameras (poor restoration quality), and even hybrid event $^+$ frame techniques (reconstruction artifacts). (bottom rows) In contrast, our generalized event cameras capture the stress ball's extensive deformations with high fidelity and an efficient readout.

Our method achieves high- quality reconstructions at 3025 FPS (96800/32) that faithfully capture non- rigid deformations, with only 431 bits per second per pixel (bps/pixel) readout, which is a $227\times$ compression (96800/431) of the raw SPAD capture. Viewed differently, for a 1 MPixel array, we would obtain a bitrate of 431 Mbps, implying that we can read off these 3025 FPS reconstructions over USB 2.0 (which supports transfer speeds of up to 480 Mbps).

Event imaging in low light. Fig. 6 compares the low- light performance of frame- based, event- based, and a generalized event camera on an urban night- time scene at 7 lux (lux measured at the sensor). For frame- based cameras, a short exposure that preserves motion may be too noisy, while a long exposure can be severely blurred. The Prophesee's performance deteriorates in low light, resulting in blurred temporal gradients. EDI++, benefiting from the idealized SPAD- based implementation, can image this scene, but finer details like the motorcyclist are lost. Our generalized event cameras, on the other hand, provide reconstructions with minimal noise, blur, or artifacts- while retaining the bandwidth efficiency of event- based systems. The compression here is $307\times$ with respect to raw SPAD outputs.

Figure 6. Event imaging in urban nighttime (7 lux, sensor side). (left to right) Low-light conditions necessitate long exposures in frame-based cameras, resulting in unwanted motion blur. The Prophesee EVK4 suffers from severe degradation in low light, causing E2VID+ to fail. Running EDI++ on perfectly aligned SPAD-frames and -events improves overall restoration quality but still gives failures on fast-moving objects. Our generalized events recover significantly more detail in low light, as seen in the inset of the motorcyclist.

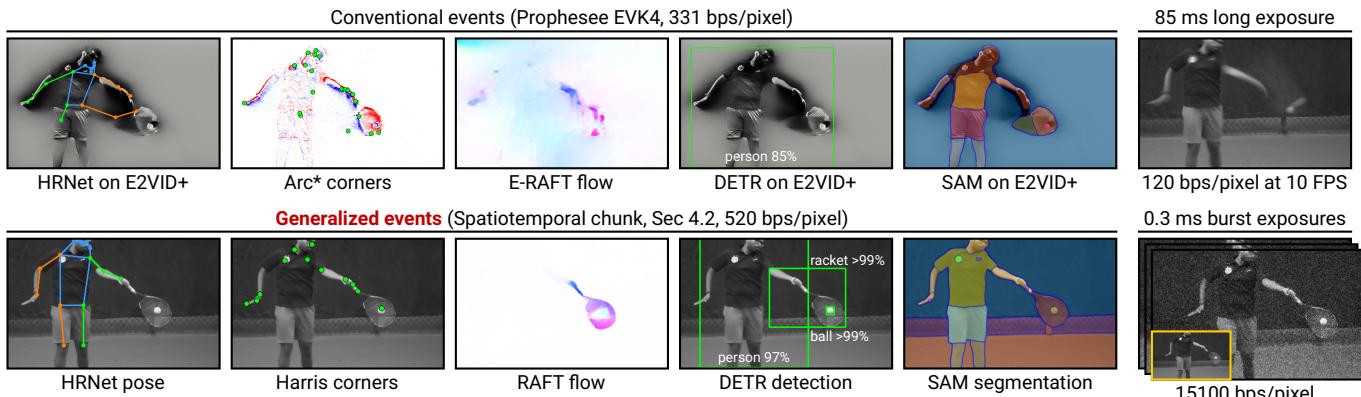
Figure 7. Plug-and-play inference on a tennis scene. (top left) Conventional events encode temporal-gradient polarities; this lossy representation limits performance on downstream tasks. (bottom left) Generalized events encode rich scene-intensity information, with a readout comparable existing event cameras. They facilitate high-quality plug-and-play inference, without requiring dedicated algorithms. (right) Generalized event cameras give image quality comparable to burst photography techniques that have a much higher readout rate.

5.2. Plug-and-Play Inference

Generalized event cameras preserve scene intensity, which enables plug- and- play event- based vision. We consider a tennis sequence (of 8196 binary frames) containing a range of object speeds. We evaluate a range of tasks: pose estimation (HRNet [59]), corner detection [18], optical flow (RAFT [61]), object detection (DETR [11]), and segmentation (SAM [32]). We compare against event- based methods applied to Prophesee events; we use Arc* [3] for corner detection and E- RAFT [16] for optical flow. For the remaining tasks, which do not have equivalent event methods, we run HRNet, DETR, and SAM on E2VID+ reconstructions.

As Fig. 7 (top left) shows, traditional events are bandwidth efficient (331 bps/pixel), but do not provide sufficient information for successful inference. Generalized events (bottom left) have a modestly higher readout (520 bps/pixel), but support accurate inference without requiring dedicated algorithms. To provide context for these rates, we compare them against frame- based methods (right). A long exposure (120 bps/pixel) blurs out the racket. Burst methods [19] recover a sharp image from a stack of short exposures, but with a large readout of 15100 bps/pixel.

5.3. Rate-Distortion Analysis

Each method in Sec. 4 features a sensitivity parameter that controls the sensor readout rate (event rate), which in turn influences image quality. In this subsection, we evaluate the impact of readout on image quality (PSNR) by performing a rate- distortion analysis. For ground truth, we use a set of YouTube- sourced high- speed videos captured by a Phantom Flex4k at 1000 FPS; see the supplement for thumbnails and links. We upsample these videos to the SPAD's frame rate and then simulate 4096 binary frames using the image formation model described in Eq. (4). When computing readout for our methods, we assume that events encode 10- bit values and account for the header bits of each event packet.

As baselines, we consider EDI++, a long exposure, compressive sensing with 8- bucket masks, and burst denoising [19] using 32 short exposures. As Fig. 8 shows, generalized event cameras provide a pronounced 4- 8 dB PSNR improvement over baseline methods. Further, our methods can compress the raw SPAD response by around $80\times$ before a noticeable drop- off in PSNR is observed.

Among our methods, the spatiotemporal chunk approach of

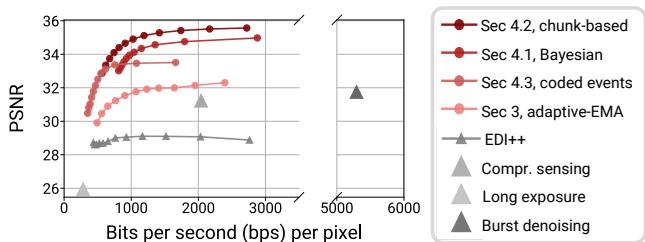
Figure 8. Rate-distortion evaluation. Our techniques feature a tunable parameter that controls the output event rate. Generalized events offer a 4–8 dB improvement in PSNR over EDI++ (at the same readout), and can compress raw photon data by $80\times$ .

Sec. 4.2 gives the best PSNR, followed by the Bayesian method (Sec. 4.1) and coded- exposure events (Sec. 4.3). That said, all methods are fairly similar in terms of rate- distortion (e.g., all three give comparable results for the scenes in Secs. 5.1 and 5.2). The methods are better distinguished by their practical characteristics. The Bayesian method gives single- photon temporal resolution; however, as we show in Sec. 5.4, it is the most expensive to compute on- chip. The chunk- based method occupies a middle ground in terms of latency and cost. Coded- exposure events have the highest latency—events are generated only every $\sim 256–512$ binary frames—but the lowest on- chip cost. This provides an end user the flexibility to choose from the space of generalized event cameras based on the latency requirements and the compute constraints of the target application.

5.4. On-Chip Feasibility and Validation

A critical limitation of single- photon sensors is the exorbitant bandwidth and power costs involved in reading off raw photon detections. However, the lightweight nature of our event camera designs allows us to sidestep this limitation by performing computations on- chip. We demonstrate that our methods are feasible on UltraPhase [4], a SPAD compute platform. UltraPhase consists of $3\times 6$ compute cores, each of which is associated with $4\times 4$ pixels.

We implement our methods for UltraPhase using custom assembly code. Some methods require minor modifications due to instruction- set limitations; see the supplement for details. We process 2500 SPAD frames from the tennis sequence used in Sec. 5.2, cropped to the UltraPhase array size of $12\times 24$ pixels. We determine the number of cycles required to execute the assembly code and estimate the chip's power consumption and readout bandwidth.

All our proposed methods run comfortably within the chip's compute budget of 4202 cycles per binary frame and its memory limit of 4 Kibit per core. As seen in Fig. 9, compared to raw photon- detection readout, our techniques reduce both bandwidth and power costs by over two orders of magnitude. The coded- exposure method is particularly efficient; on most binary frames, it only requires multiplying a binary code with incident photon detections. Our proof- of- concept evaluation may pave the way for future near- sensor implementations of generalized event

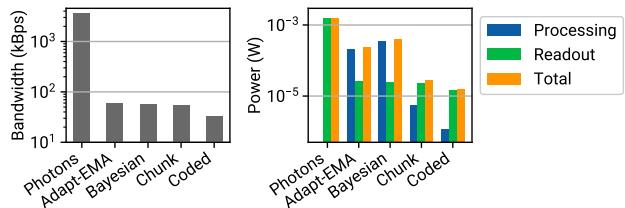
Figure 9. On-chip compatibility. We validate the feasibility of our approach on UltraPhase [4], a computational SPAD imager. Compared to reading out raw photon data, all of our approaches give marked reductions in both bandwidth (left) and power (right).

Figure 10. Limitations and failure modes. (left) Our reconstructions (yellow inset) on dynamic scenes with rigid objects can be inferior to burst photography (green inset). (center) Modulated light sources, such as this phone screen, can trigger a deluge of events (change points shown in the inset). (right) Rapid camera motion can result in an event rate divergent from scene dynamics.

cameras, which with advances in chip- to- chip communication, could involve a dedicated “photon processing unit”, similar to a camera image signal processor (ISP).

6. Limitations and Discussion

Generalized events push the frontiers of event- based imaging; however, some scenarios lead to sub- optimal performance. As seen in Fig. 10 (left), if the scene dynamics is entirely comprised of rigid motion, burst photography [36] gives better image quality, albeit with much higher readout. (middle) Similar to current event cameras, modulated light sources trigger unwanted events that reduce bandwidth savings. However, it may be possible to ignore some of these events, perhaps by modeling the lighting variations [55].

Ego- motion events. Camera motion can trigger events in static regions, although our methods still yield substantial compression ( $130\times$ over SPAD outputs, Fig. 10 right). We analyze the impact of ego- motion on bandwidth savings further in the supplement. However, single- photon cameras can emulate sensor motion by integrating flux along alternate spatiotemporal trajectories [60]. We can imagine a generalized event camera that is “ego- motion compensated,” by computing events along a suitable trajectory.

Photon- stream compression. SPADs generate a torrent of data—e.g., 12.5 GBps for a MPixel array at $100\mathrm{kHz}$ —that can easily overwhelm data interfaces. Generalized event cameras reduce readout by around two orders of magnitude, by decoupling readout from the SPAD’s frame rate and instead basing it on scene dynamics. This could pave the way for practical, high- resolution single- photon sensors.

References

[1] Ryan Prescott Adams and David JC MacKay. Bayesian online changepoint detection. arXiv preprint arXiv:0710.3742, 2007. 4 [2] Reda Alami, Odalric Maillard, and Raphael Feraud. Restarted bayesian online change- point detector achieves optimal detection delay. In International conference on machine learning, pages 211- 221. PMLR, 2020. 4, 5 [3] Ignacio Alzugaray and Margarita Chli. Asynchronous corner detection and tracking for event cameras in real time. IEEE Robotics and Automation Letters, 3(4):3177- 3184, 2018. 7 [4] Andrei Ardelean. Computational Imaging SPAD Cameras. PhD thesis, Ecole polytechnique federale de Lausanne, 2023. 2, 6, 8 [5] Souptik Barua, Yoshitaka Miyatani, and Ashok Veeraraghavan. Direct face detection and video reconstruction from event cameras. In WACV, pages 1- 9. IEEE, 2016. 3 [6] Raphael Berner, Christian Brandli, Minhao Yang, S- C Liu, and Tobi Delbruck. A 240x180 120dB 10mW 12us- latency sparse output vision sensor for mobile applications. In Proceedings of the International Image Sensors Workshop, number CONF, pages 41- 44, 2013. 1, 2 [7] Anthony Bisulco, Fernando Cladera Ojeda, Volkan Isler, and Daniel D Lee. Fast motion understanding with spatiotemporal neural networks and dynamic vision sensors. In 2021 IEEE International Conference on Robotics and Automation (ICRA), pages 14098- 14104. IEEE, 2021. 1 [8] Assim Boukhayma, Arnaud Peizerat, and Christian Enz. A sub0.5 electron read noise VGA image sensor in a standard CMOS process. IEEE Journal of Solid- State Circuits, 2016. 4 [9] Christian Brandli, Raphael Berner, Minhao Yang, Shih- Chi Liu, and Tobi Delbruck. A $240\times 180$ 130 dB $3\mu \mathrm{s}$ latency global shutter spatiotemporal vision sensor. IEEE Journal of Solid- State Circuits, 49(10):2333- 2341, 2014. 2, 3 [10] Christian Brandli, Lorenz Muller, and Tobi Delbruck. Realtime, high- speed video decompression using a frame- and eventbased DAVIS sensor. In 2014 IEEE International Symposium on Circuits and Systems (ISCAS), pages 686- 689. IEEE, 2014. 3 [11] Nicolas Carion, Francisco Massa, Gabriel Synnaeve, Nicolas Usunier, Alexander Kirillov, and Sergey Zagoruyko. End- toend object detection with transformers. In Computer Vision - ECCV 2020, pages 213- 229, Cham, 2020. Springer International Publishing. 7 [12] Andrea Censi and Davide Scaramuzza. Low- latency event- based visual odometry. In 2014 IEEE International Conference on Robotics and Automation (ICRA), pages 703- 710. IEEE, 2014. 1 [13] Matthew Cook, Luca Gugelmann, Florian Jug, Christoph Krautz, and Angelika Steger. Interacting maps for fast visual interpretation. In The 2011 International Joint Conference on Neural Networks, pages 770- 776, 2011. 3 [14] Yue Gao, Siqi Li, Yipeng Li, Yandong Guo, and Qionghai Dai. Superfast: $200\times$ video frame interpolation via event camera. IEEE TPAMI, 45(6):7764- 7780, 2023. 1 [15] Daniel Gehrig, Henri Rebecq, Guillermo Gallego, and Davide Scaramuzza. EKLT: Asynchronous photometric feature tracking using events and frames. IJCV, 128(3):601- 618, 2020. 1 [16] Mathias Gehrig, Mario Millhausler, Daniel Gehrig, and Davide Scaramuzza. E- raft: Dense optical flow from event cameras. In 2021 International Conference on 3D Vision (3DV), pages

197- 206. IEEE, 2021. 7 [17] Istvan Gyongy, Neale AW Dutton, and Robert K Henderson. Single- photon tracking for high- speed vision. Sensors, 18(2):323, 2018. 3 [18] Chris Harris, Mike Stephens, et al. A combined corner and edge detector. In Alvey vision conference, pages 10- 5244. Citeseer, 1988. 7 [19] Samuel W. Hasinoff, Dillon Sharlet, Ryan Geiss, Andrew Adams, Jonathan T. Barron, Florian Kainz, Jiawen Chen, and Marc Levoy. Burst photography for high dynamic range and low- light imaging on mobile cameras. ACM TOG, 35(6):1- 12, 2016. 7 [20] Botao He, Haojia Li, Siyuan Wu, Dong Wang, Zhiwei Zhang, Qianli Dong, Chao Xu, and Fei Gao. Fast- dynamic- vision: Detection and tracking dynamic objects with event and depth sensing. In 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 3071- 3078. IEEE, 2021. 1 [21] Javier Hidalgo- Carrio, Guillermo Gallego, and Davide Scaramuzza. Event- aided direct sparse odometry. In CVPR, pages 5781- 5790, 2022. 1 [22] Yasunobu Hitomi, Jinwei Gu, Mohit Gupta, Tomoo Mitsunaga, and Shree K. Nayar. Video from a single coded exposure photograph using a learned over- complete dictionary. In 2011 International Conference on Computer Vision, pages 287- 294, 2011. 5 [23] Jing Huang, Menghan Guo, and Shoushun Chen. A dynamic vision sensor with direct logarithmic output and full- frame pictureon- demand. In 2017 IEEE International Symposium on Circuits and Systems (ISCAS), pages 1- 4, 2017. 2 [24] Zhewei Huang, Tianyuan Zhang, Wen Heng, Boxin Shi, and Shuchang Zhou. Real- time intermediate flow estimation for video frame interpolation. In Proceedings of the European Conference on Computer Vision (ECCV), 2022. 6 [25] Jorge Igual. Photographic noise performance measures based on raw files analysis of consumer cameras. Electronics, 8(11):1284, 2019. 4 [26] Atul Ingle, Andreas Velten, and Mohit Gupta. High Flux Passive Imaging With Single- Photon Sensors. In CVPR, 2019. 3 [27] Atul Ingle, Trevor Seets, Mauro Buttafava, Shantanu Gupta, Alberto Tosi, Mohit Gupta, and Andreas Velten. Passive interphoton imaging. In CVPR, 2021. 3 [28] Kiyotaka Iwabuchi, Yusuke Kameda, and Takayuki Hamamoto. Image quality improvements based on motion- based deblurring for single- photon imaging. IEEE Access, 9:30080- 30094, 2021. 3 [29] Nikita Karaev, Ignacio Rocco, Benjamin Graham, Natalia Neverova, Andrea Vedaldi, and Christian Rupprecht. CoTracker: It is better to track together. 2023. [30] Anthony Kay. Tesseract: an open- source optical character recognition engine. Linux Journal, 2007(159):2, 2007. [31] Hanme Kim, Ankur Handa, Ryad Berosman, Sio- Hoi Ieng, and Andrew J Davison. Simultaneous mosaicing and tracking with an event camera. Proc. Brit. Mach. Vis. Conf, 43:566- 576, 2014. 3 [32] Alexander Kirillov, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao, Spencer Whitehead, Alexander C. Berg, Wan- Yen Lo, Piotr Dollar, and Ross Girshick. Segment anything, 2023. 7 [33] Haolong Li and Joerg Stueckler. Tracking 6- DoF object motion from events and frames. In 2021 IEEE International Conference

on Robotics and Automation (ICRA), pages 14171- 14177. IEEE, 2021. 1[34] P Lichtsteiner. 64x64 event- driven logarithmic temporal derivative silicon retina. In Program 2003 IEEE Workshop on CCD and AIS, 2003. 1, 2, 4[35] Yuhao Liu, Felipe Gutierrez- Barragan, Atul Ingle, Mohit Gupta, and Andreas Velten. Single photon camera guided extreme dynamic range imaging. In WACV, pages 1575- 1585, 2022. 3[36] Sizhuo Ma, Shantanu Gupta, Arin C. Ulku, Claudio Bruschini, Edoardo Charbon, and Mohit Gupta. Quanta burst photography. ACM TOG, 39(4):1- 16, 2020. 3, 8[37] Sizhuo Ma, Paul Mos, Edoardo Charbon, and Mohit Gupta. Burst vision using single- photon cameras. In WACV, pages 5375- 5385, 2023. 3[38] Kazuhiro Morimoto, Andrei Ardelean, Ming- Lo Wu, Arin Can Ulku, Ivan Michel Antolovic, Claudio Bruschini, and Edoardo Charbon. Megapixel time- gated SPAD image sensor for 2D and 3D imaging applications. Optica, 7(4):346- 354, 2020. 4[39] Gottfried Munda, Christian Reinbacher, and Thomas Pock. Real- time intensity- image reconstruction for event cameras using manifold regularisation. IJCV, 126:1381- 1393, 2018. 3[40] Shuichi Namiki, Shunichi Sato, Yusuke Kameda, and Takayuki Hamamoto. Imaging method using multi- threshold pattern for photon detection of quanta image sensor. In International Workshop on Advanced Imaging Technology (IWAIT) 2022, page 1217702. SPIE, 2022. 3[41] Liyuan Pan, Cedric Scheerlinck, Xin Yu, Richard Hartley, Miaomiao Liu, and Yuchao Dai. Bringing a blurry frame alive at high frame- rate with an event camera. In CVPR, 2019. 3[42] Liyuan Pan, Richard Hartley, Cedric Scheerlinck, Miaomiao Liu, Xin Yu, and Yuchao Dai. High frame rate video reconstruction based on an event camera. IEEE TPAMI, 44(5):2519- 2533, 2022. 6[43] Federico Paredes- Valles and Guido C. H. E. de Croon. Back to event basics: Self- supervised learning of image reconstruction for event cameras via photometric constancy. In CVPR, pages 3446- 3455, 2021. 3[44] Christoph Posch, Daniel Matolin, and Rainer Wohlgenannt. A QVGA 143 dB dynamic range frame- free pwm image sensor with lossless pixel- level video compression and time- domain cds. IEEE Journal of Solid- State Circuits, 46(1):259- 275, 2011. 1, 2[45] Ramesh Raskar, Amit Agrawal, and Jack Tumblin. Coded exposure photography: motion deblurring using fluttered shutter. In Acm Siggraph 2006 Papers, pages 795- 804. 2006. 5[46] Henri Rebecq, Rene Ramfl, Vladlen Koltun, and Davide Scaramuzza. High speed and high dynamic range video with an event camera. IEEE TPAMI, 2019. 3[47] Dikpal Reddy, Ashok Veeraraghavan, and Ramu Chellappa. P2C2: Programmable pixel compressive camera for high speed imaging. In CVPR 2011, pages 329- 336, 2011. 5[48] Alexis Rochas. Single photon avalanche diodes in cmos technology. Technical report, Citeseer, 2003. 4[49] Nitin J Sanket, Chethan M Parameshwara, Chahat Deep Singh, Ashwin V Kuruttukulam, Cornelia Fermiller, Davide Scaramuzza, and Yiannis Abimonos. Evdodgenet: Deep dynamic obstacle dodging with event cameras. In 2020 IEEE International Conference on Robotics and Automation (ICRA), pages 10651- 10657. IEEE, 2020. 1

[50] Cedric Scheerlinck, Nick Barnes, and Robert Mahony. Continuous- time intensity estimation using event cameras. In ACCV, pages 308- 324. Springer, 2018. 3[51] Cedric Scheerlinck, Henri Rebecq, Daniel Gehrig, Nick Barnes, Robert Mahony, and Davide Scaramuzza. Fast image reconstruction with an event camera. In WACV, 2020. 3[52] Trevor Seets, Atul Ingle, Martin Laurenzis, and Andreas Velten. Motion adaptive deblurring with single- photon cameras. In WACV, pages 1945- 1954, 2021. 3[53] Prasan Shedligeri and Kaushik Mitra. Photorealistic image reconstruction from hybrid intensity and event- based sensor. Journal of Electronic Imaging, 28(6):063012- 063012, 2019. 3[54] Prasan Shedligeri, Anupama S, and Kaushik Mitra. A unified framework for compressive video recovery from coded exposure techniques. In WACV, pages 1600- 1609, 2021. 6[55] Mark Sheinin, Yoav Y. Schechner, and Kiriakos N. Kutulakos. Computational imaging on the electric grid. In CVPR, 2017. 8[56] Hyeojun Sim, Jihyong Oh, and Munchurl Kim. XVFI: extreme video frame interpolation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 14489- 14498, 2021. 6[57] Timo Stoffregen, Cedric Scheerlinck, Davide Scaramuzza, Tom Drummond, Nick Barnes, Lindsay Kleeman, and Robert Mahony. Reducing the sim- to- real gap for event cameras. In ECCV, pages 534- 549. Springer, 2020. 6[58] Binyi su, Lei Yu, and Wen Yang. Event- based high frame- rate video reconstruction with a novel cycle- event network. In ICIP, pages 86- 90, 2020. 3[59] Ke Sun, Bin Xiao, Dong Liu, and Jingdong Wang. Deep high- resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019. 7[60] Varun Sundar, Andrei Ardelean, Tristan Swedish, Claudio Bruschini, Edoardo Charbon, and Mohit Gupta. Sodacam: Software- defined cameras via single- photon imaging. In ICCV, pages 8165- 8176, 2023. 3, 6, 8[61] Zachary Teed and Jia Deng. Raft: Recurrent all- pairs field transforms for optical flow. In Computer Vision - ECCV 2020, pages 402- 419, Cham, 2020. Springer International Publishing. 7[62] Arin Can Ulku, Claudio Bruschini, Ivan Michel Antolovic, Yung Kuo, Rinat Ankri, Shimon Weiss, Xavier Michalet, and Edoardo Charbon. A $512 \times 512$ SPAD Image Sensor With Integrated Gating for Widefield FLIM. IEEE Journal of Selected Topics in Quantum Electronics, 25(1):1- 12, 2019. 2, 4, 6[63] Lishun Wang, Miao Cao, and Xin Yuan. Efficientsci: Densely connected network with space- time factorization for large- scale video snapshot compressive imaging. In CVPR, pages 18477- 18486, 2023. 6[64] Zhaohui Wang, Xiao Lin, Abhinav Mishra, and Ram Sriharsha. Online changepoint detection on a budget. In 2021 International Conference on Data Mining Workshops (ICDMW), pages 414- 420. IEEE, 2021. 5[65] Mian Wei, Sotiris Nousias, Rahul Gulve, David B. Lindell, and Kiriakos N. Kutulakos. Passive ultra- wideband single- photon imaging. In ICCV, pages 8135- 8146, 2023. 3[66] Xin Yuan, Yang Liu, Jinli Suo, Frédo Durand, and Qionghai Dai. Plug- and- play algorithms for video snapshot compressive imaging. IEEE Transactions on Pattern Analysis and Machine

Intelligence, 44(10):7093–7111, 2022. 6[67] Zelin Zhang, Anthony J Yezzi, and Guillermo Gallego. Formulating event- based image reconstruction as a linear inverse problem with deep regularization using optical flow. IEEE TPAMI, 45 (07):8372–8389, 2023. 3[68] Alex Zihao Zhu, Nikolay Atanasov, and Kostas Daniilidis. Event- based visual inertial odometry. In CVPR, 2017. 1[69] Yunhao Zou, Yinqiang Zheng, Tsuyoshi Takatani, and Ying Fu. Learning to reconstruct high speed and high dynamic range videos from events. In CVPR, pages 2024–2033, 2021. 3